考点：

• 运筹方法 ⭐️⭐️
  • 关键路径法
  • 线性规划
  • 动态规划
• 随机函数 ⭐️
• 数学建模 ⭐️

1分

1 简单运筹方法 ⭐️⭐️

1.1 关键路径法

详见项目管理-制定进度计划-关键路径法

1.2 线性规划

求多元线性函数的条件极值

方法：代入边界点

【例】某企业需要采用甲、乙、丙三种原材料生产I、II两种产品。生产两种产品所需原材料数量、单位产品可获得利润以及企业现有原材料数如下表所示，则公司可获得的最大利润是（?）万元。取得最大利润时，原材料（?）尚有剩余。
A. 21；B. 34；C. 39；D. 48
A. 甲；B. 乙；C. 丙；D. 乙和丙

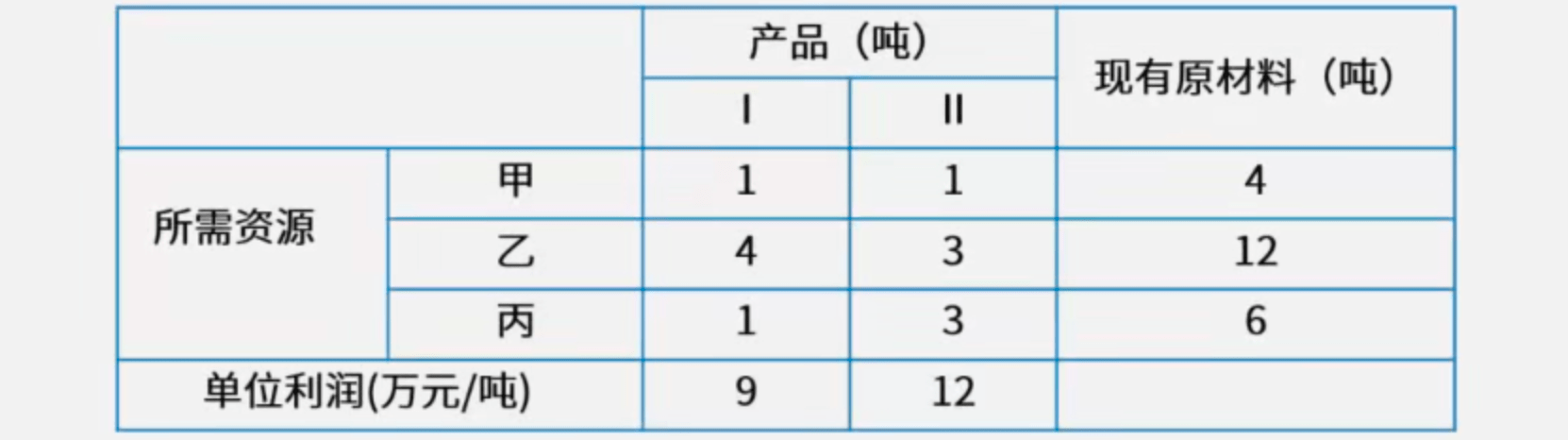
【解】设I、II产品的各自产量分别为x,y（吨），则目标函数为

W(x,y)=9x+12y

其线性约束条件为

\begin{cases}
x ≥ 0 \\
y≥0 \\
x+y≤4 \\
4x+3y≤12 \\
x+3y≤6
\end{cases}

如下图所示，深色区域即为可行域：

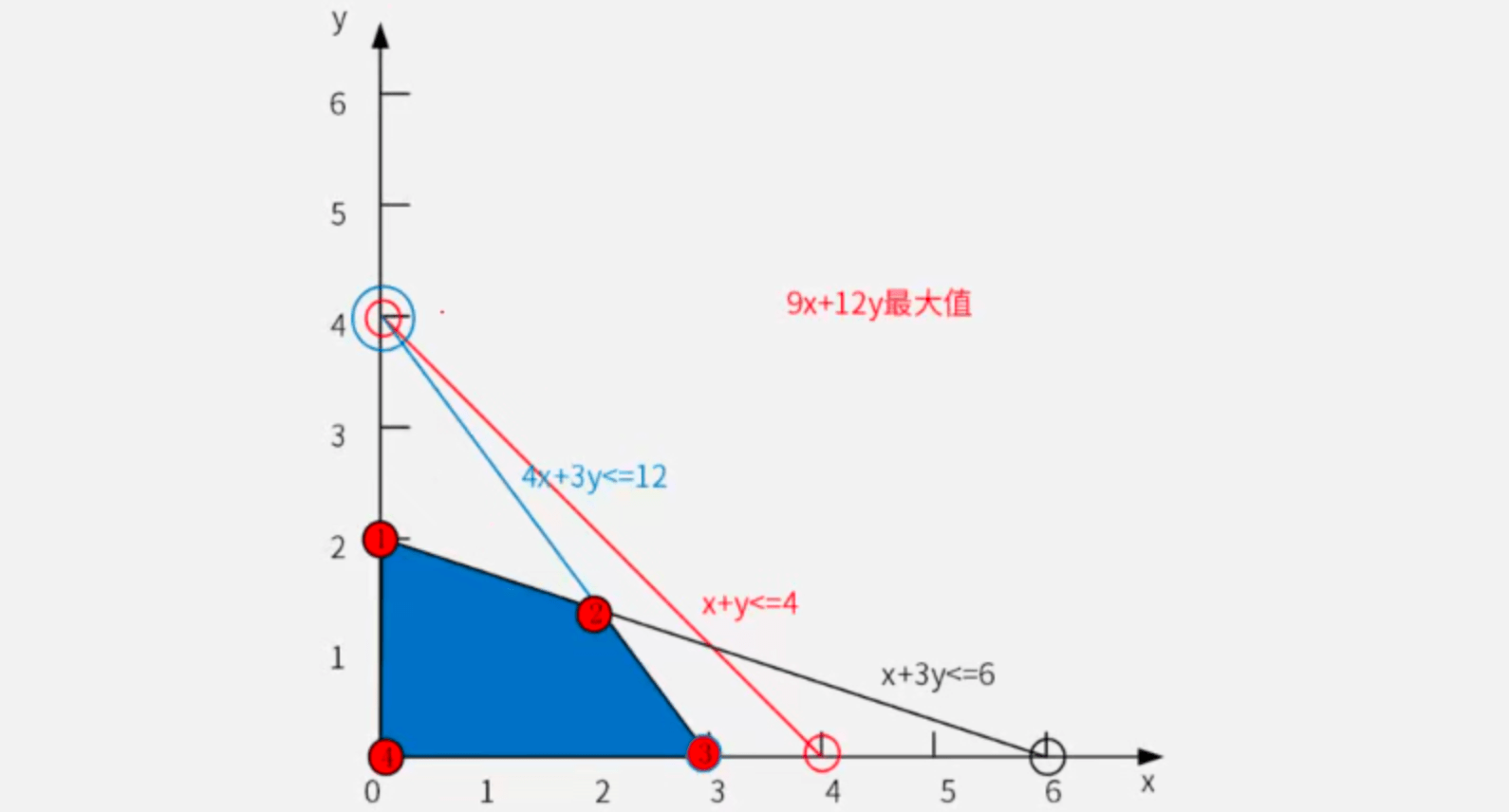
联立方程式可求得可行域各顶点坐标，其中右上角的顶点坐标为(2,\frac43)。将各坐标代入W(x,y)，得W(0,2)=24,W(2,\frac43)=34,W(3,0)=27,W(0,0)=0，故W_{\max}=34。第1问答案为B。

此时I、II产品的产量为(2,\frac43)，则消耗甲资源2+\frac43=\frac{10}{3}<4、乙资源2\times 4 + 3\times\frac43=12、丙资源2+3\times \frac43=6，故仅甲资源有剩余。第2问答案为A。

1.3 动态规划

快速求解方法：暴力枚举、贪心策略分析

【例1】某公司现有400万元用于投资甲、乙、丙三个项目，投资额以百万元为单位，已知甲、乙、丙三项投资的可能方案及相应获得的收益如下表所示，则该公司能够获得的最大收益值是（?）百万元。（A. 17；B.18；C.20；D.21）

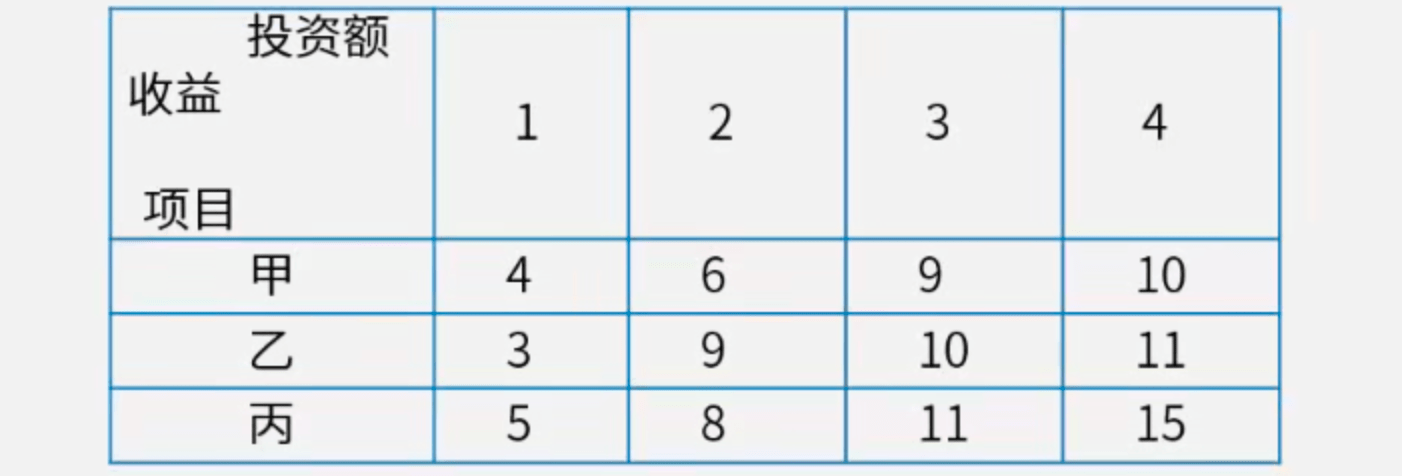
【解】用(甲,乙,丙)三元组表示所选的投资额分配组合。
暴力求解：枚举全部情况！！！可得最大收益额为18。答案为B。

【例2】某公司打算向它的三个营业区增设6个销售店，每个营业区至少增设1个。各营业区年增加的利润与增设的销售店个数有关，具体关系如表所示。可以调整各营业区增设的销售店的个数，使公司总利润增加额最大达（?）万元。（A. 520；B. 490；C. 470；D. 510）

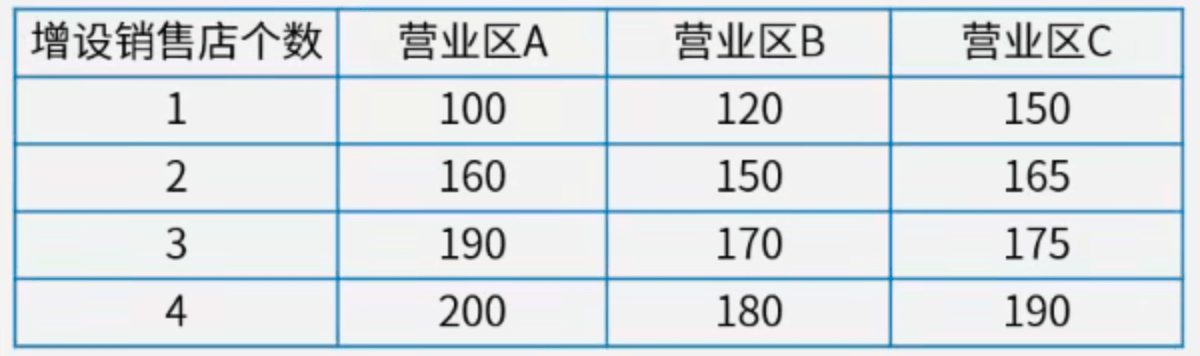
【解】用(A,B,C)三元组表示各营业区增设的销售店情况，注意本题每个营业区至少增设1个。
同例1，暴力求解：枚举全部情况！！！可得总利润增加额最大为490万元。答案为B。

【例3】某企业准备将四个工人甲、乙、丙、丁分配在A、B、C、D四个岗位。每个工人由于技术水平不同，在不同岗位上每天完成任务所需的工时见下表。适当安排岗位，可使四个工人以最短的总工时（?）全部完成每天的任务。（A. 13；B. 14；C. 15；D. 16）

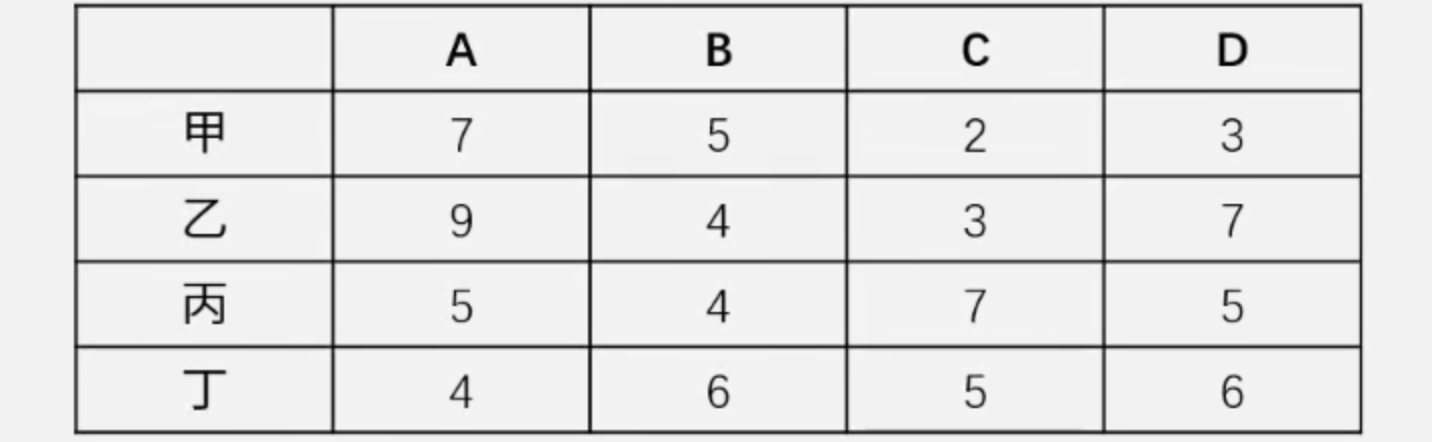
【解】本题暴力列举极为麻烦，因此考虑贪心策略分析。
先从A开始，想让A工时最短应给丁，此时对于B、C、D最优选择分别为乙或丙、甲、甲。C、D发生冲突，因此权衡双方“让步损失”所得出的最优调整方案为C给乙、D给甲，与此同时可得B给丙。
因此可得最短总工时为14。答案为B。

---

2 随机函数 ⭐️

方法：模拟随机数（计算机编程实现）、转化为长度/面积/体积比

【例】1路和2路公交车都将在10分钟内均匀随机地到达同一车站，则它们相隔4分钟内到达该站的概率为（?）。（A. 0.36；B. 0.48；C. 0.64；D. 0.76）

【解】分别以1路和2路公交车的到站时间点为x,y轴坐标，建立xOy坐标系

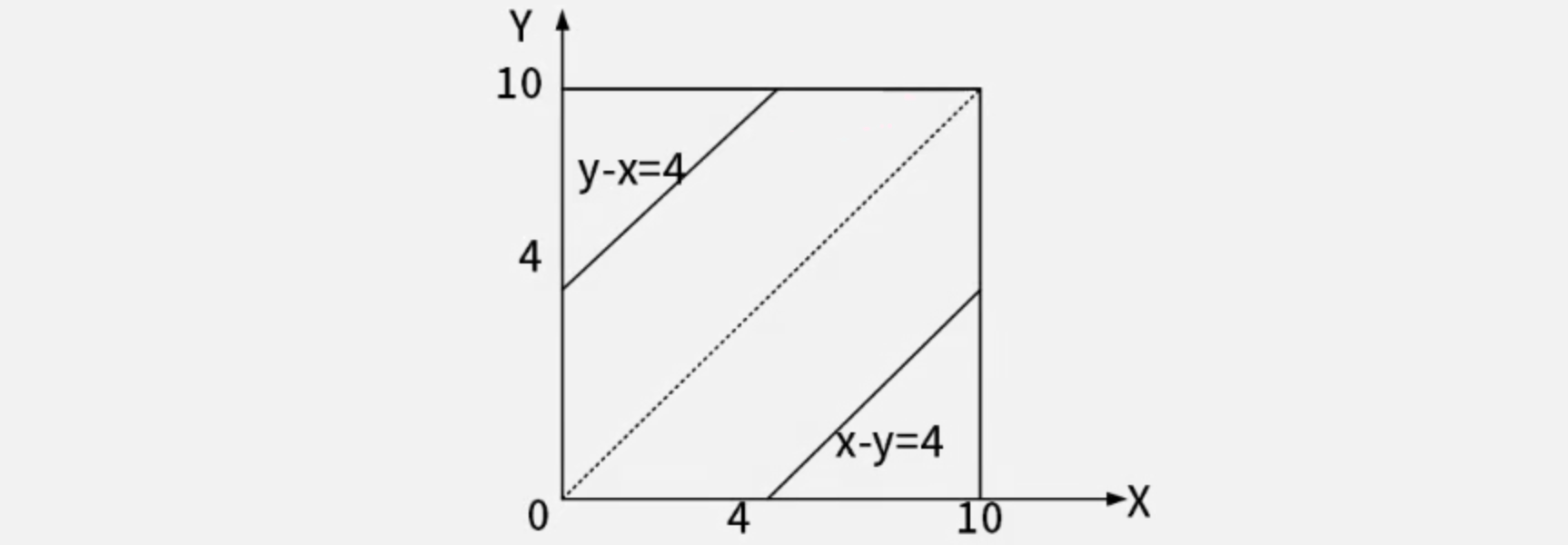
由已知得，x\in[0,10],y\in[0,10]，即所有可能情况的点组成如图所示的正方形区域（记为D）。符合“两车相隔4分钟内到达该站”条件的(x,y)满足

\begin{cases}
x-y≤4 \\
y-x≤4
\end{cases}

即该正方形边框与直线x-y=4,y-x=4所围成的区域（记为D_1）。因此将概率比转换为面积比可以求得

P=\frac{S_{D_1}}{S_D}=\frac{10\times 10-2\times \frac12 \times 6\times 6}{10\times 10}=0.64

答案为C。

---

3 数学建模 ⭐️

数学建模（Mathematics Modeling）是一种数学的思考方法，是运用数学的语言和方法，通过抽象和简化，建立能近似刻画并解决实际问题的模型的一种强有力的数学手段。

数学建模的过程：

1. 模型准备：了解问题的实际背景，明确其实际意义，掌握对象的各种信息用数学语言来描述问题。
2. 模型假设：根据实际对象的特征和建模的目的，对问题进行必要的简化，并用精确的语言提出一些恰当的假设。
3. 模型建立：在假设的基础上，利用适当的数学工具来刻划各变量之间的数学关系，建立相应的数学结构。只要能够把问题描述清楚，尽量使用简单的数学工具。
4. 模型求解：利用获取的数据资料，对模型的所有参数做出计算（估计）。
5. 模型分析：对所得的结果进行数学上的分析。
6. 模型检验：将模型分析结果与实际情形进行比较，以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合，则要对计算结果给出其实际含义，并进行解释。如果模型与实际吻合较差，则应该修改假设，再次重复建模过程。
7. 模型应用：应用方式因问题的性质和建模的目的而异。

模型分析：

1. 模型的合理性分析：最佳、适中、满意等
2. 模型的误差分析：模型误差、观测误差、截断误差、舍入误差、过失误差、绝对误差、相对误差等
3. 参数的灵敏性分析：变量数据是否敏感，在最优方案不变的条件下这些变量允许变化的范围

模型检验：

• 利用实际案例数据对模型进行检验。将模型作为一个黑盒，通过案例数据的输入，检查其输出是否合理。这是应用人员常用的方法。
• 可以请专家来分析模型是否合理。经验丰富的专家一般会根据模型自身的逻辑，再结合实际情况，分析是否会出现矛盾或问题。
• 利用计算机来模拟实际问题，再在计算机上检验该数学模型。有时很难用实际案例或聘请专家来检验模型，例如试验或实验的代价太大，难以取得实际案例，有的项目技术比较新，缺乏有经验的专家。又例如对某种核辐射防护建立的数学模型，采用计算机模拟方法来检验就十分有效。

数学建模方法：

1. 直接分析法：认识原理，直接构造出模型。
2. 类比法：根据类似问题模型构造新模型。
3. 数据分析法：大量数据统计分析之后建模。
4. 构想法：对将来可能发生的情况给出设想从而建模。

---

4 图论

专业教程：数据结构强化笔记

4.1 最小生成树

最小生成树（Minimum Spanning Tree，MST）的特点：

1. 所有顶点接入
2. 没有回路
3. 权值之和最小

常用算法：Prim算法（加点法）、Kruskal算法（加边法）

【例】某小区有七栋楼房①~⑦（见下图），各楼房之间可修燃气管道路线的长度（单位：百米）已标记在连线旁。为修建连通各个楼房的燃气管道，该小区内部煤气管道的总长度至少为多少百米？

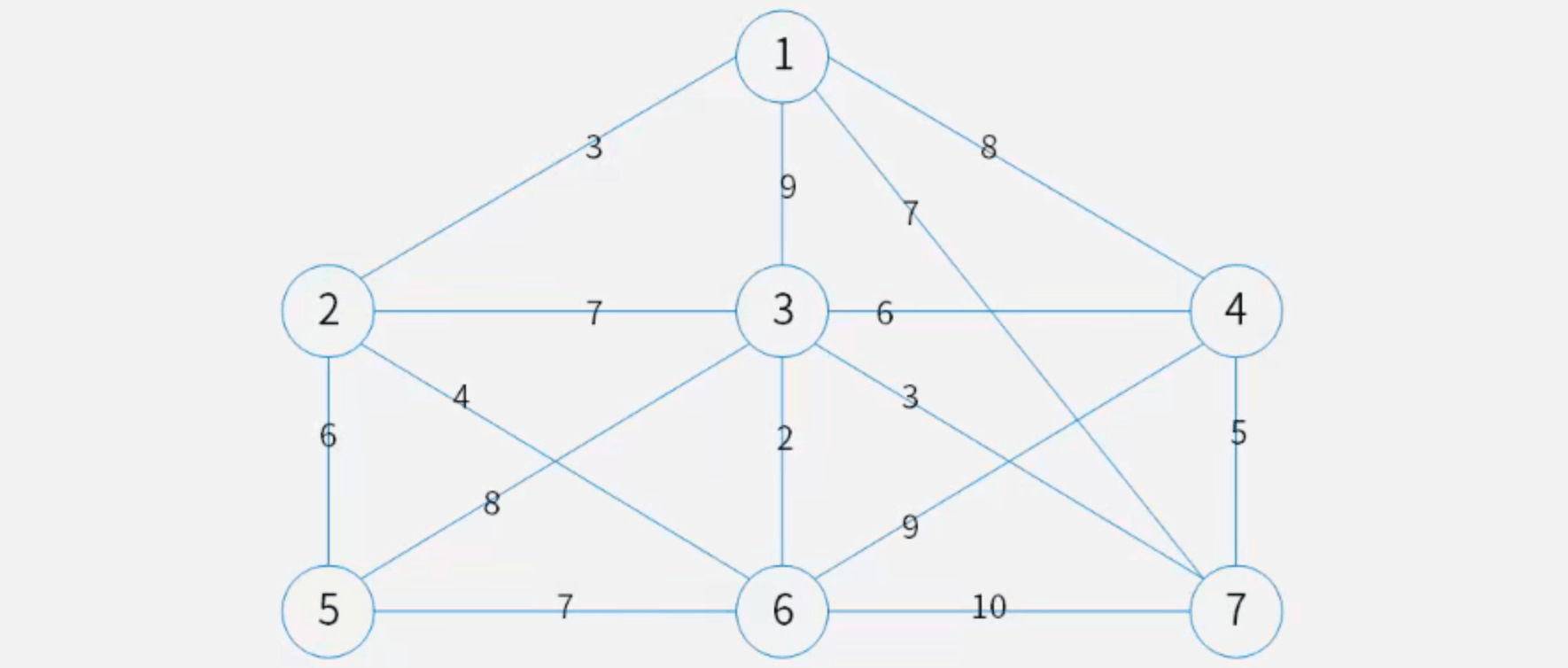
【解】任选Prim算法、Kruskal算法进行求解，答案为23。

4.2 最短路径

常用算法：Dijkstra算法、Floyd算法

【例】有一批货物要从城市s发送到城市t（如下图所示），线条上的数字代表通过这条路的费用（单位为万元）。运送这批货物至少需要花费多少元？

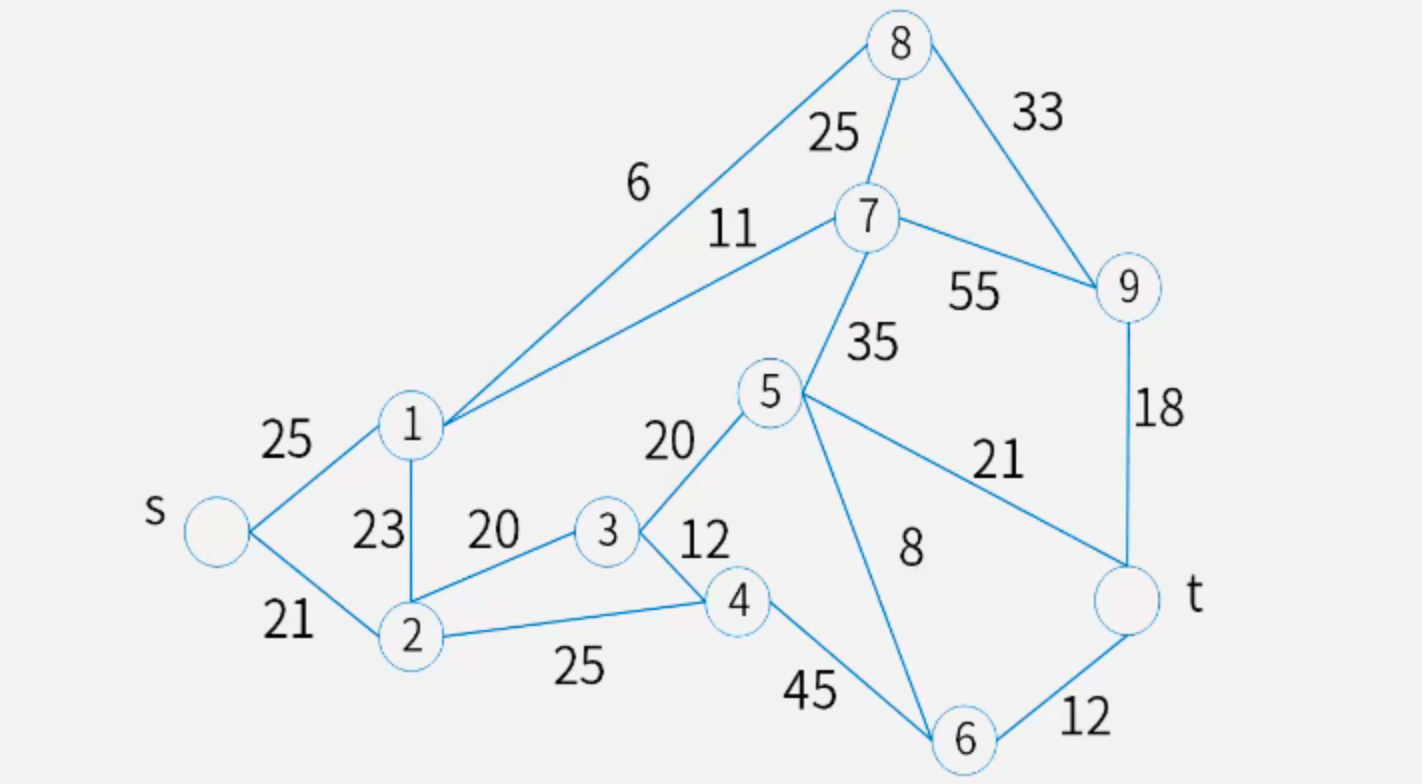
【解】使用Dijkstra算法可求得最短路径为s → 2 → 3 → 5 → 6 → t。答案即为边权之和，为81元。

4.3 网络与最大流量

最大流量由瓶颈决定。

方法：抽取分析

【例】下图标出了某地区的运输网，各节点之间的运输能力如下表所示。从节点①到节点⑥的最大运输能力（流量）可达到多少万吨/小时？

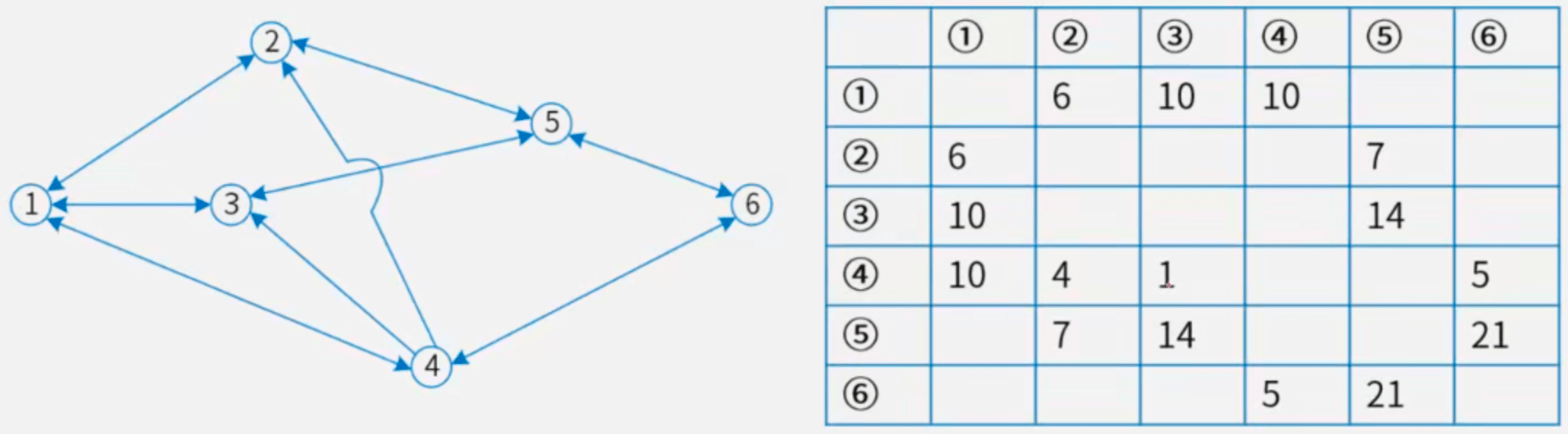
【解】将表中参数在图中标注，如下所示

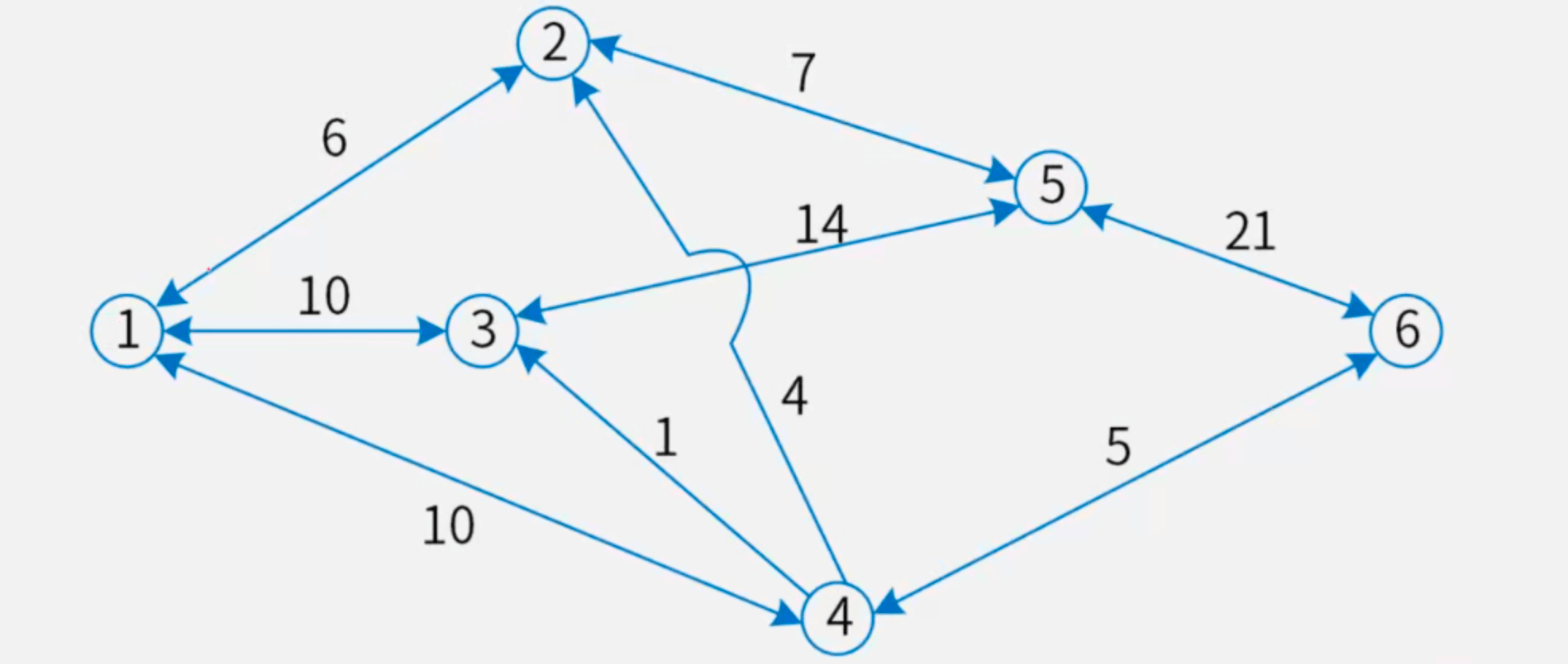
同动态规划的快速求解方法，使用类似贪心策略分析的抽取分析求解：

• 列举出所有线路并分析流量，可以得出第1条线路为1 → 3 → 5 → 6，流量为10
• 将该路线阻塞（各边的运输能力减去刚所求得的流量，即被“抽取边”），重复上一步
• 反复执行上述过程，直至所有路径均被抽走。

最后可得答案为10+6+5+1+1=23。

---

5 决策

决策（Decision-making）过程中的组成：

• 決策者
• 可供选择的方案
• 衡量选择方案的准则
• 事件
• 每一事件的发生将会产生的某种结果
• 决策者的价值观

决策的分类：

1. 确定型决策
2. 风险決策
3. 不确定型决策

5.1 不确定型决策

常见的不确定型决策准则（Criterion）：

1. 乐观主义准则（maxmax准则）：“大中取大”，总抱有乐观和冒险的态度，决不放弃任何获得最好结果的机会。在决策表中各个方案对各个状态的结果中选出最大者，记在表的最右列，再从该列中选出最大者。
2. 悲观主义准则（maxmin准则）：“小中取大”。抱有悲观和保守的态度，在各种最坏的可能结果中选择最好的。决策时从决策表中各方案对各个状态的结果选出最小者，记在表的最右列，再从该列中选出最大者。
3. 折中主义准则（Harwicz准则）：既不乐观冒险，也不悲观保守，而是从中折中平衡，用折中系数α来表示，井规定0≤\alpha≤1，cv_i=\alpha \max\{a_{ij}\}+(1-\alpha)\min\{a_{ij}\}，再比较cv_i，选择其中最大者。（考得极少）
4. 等可能准则（Laplace准则）：当决策者无法事先确定每个自然状态出现的概率时，可以将每个状态出现的概率定为\frac1n（等可能），然后按照EMV（最大期望收益准则，Expected Monetary Value）决策。
5. 后悔值准则（Savage准则）：每个自然状态的最大收益值（损失矩阵取为最小值）作为该状态的理想目标，并将该状态的其它值与最大值的差作为未达到理想目标的后悔值（当趋势确定后，哪种策略最合适则其后悔值为0，其他策略据此计算相应亏损即后悔值）。决策的原则是最大后悔值达到最小（minmax，大中取小，最小最大后悔值）

不确定型决策时常使用决策矩阵（Decision Matrix）：

5.2 决策表与决策树

决策树（Decision Tree）与决策表（Decision Table）均为风险决策时的有效工具。

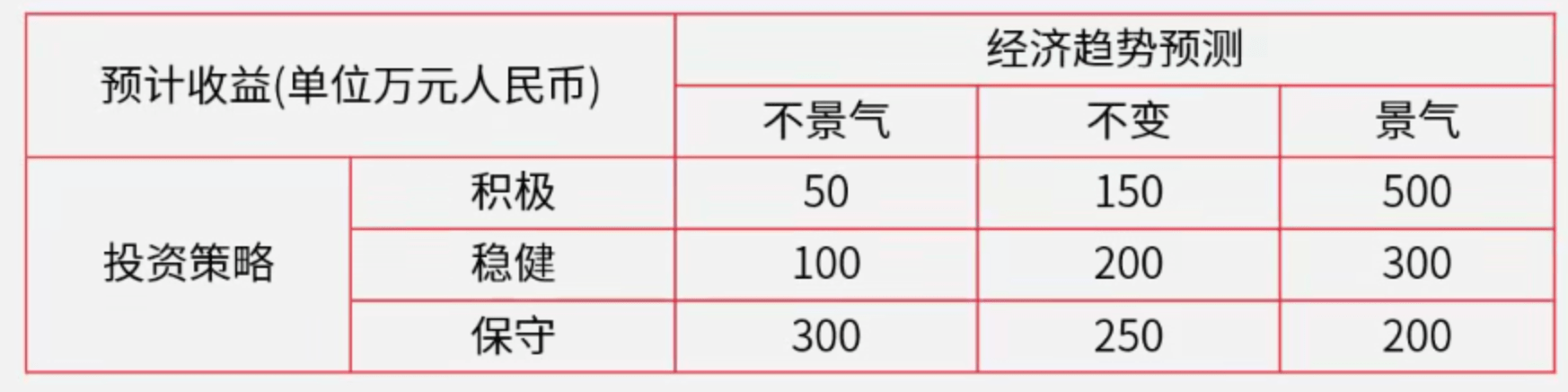
【例1】某电子商务公司要从A地向B地的用户发送一批价值为90000元的货物。从A地到B地有水、陆两条路线。走陆路时比较安全，其运输成本为10000元；走水路时一般情况下的运输成本只要7000元，不过一旦遇到暴风雨天气，则会造成相当于这批货物总价值的10%的损失。根据历年情况，这期间出现暴风雨天气的概率为1/4，那么该电子商务公司该如何选择？
【解】建立如下决策树，分别求加权平均即可

水路：7000\times 75\%+(7000+90000\times 10\%)\times 25\%=9250
陆路：10000\times 75\%+10000\times25\%=10000
水路成本低于陆路，故应选水路。

【例2】评估和选择最佳系统设计方案时，甲认为可以采用点值评估方法，即根据每一个价值因素的重要性，综合打分来选择最佳的方案。乙根据甲的提议，对如下表所示的系统A和B进行评估，那么乙认为（?）。
A. 最佳方案是A；B. 最佳方案是B；C. 条件不足，不能得出结论；D．只能用成本/效益分析方法做出判断

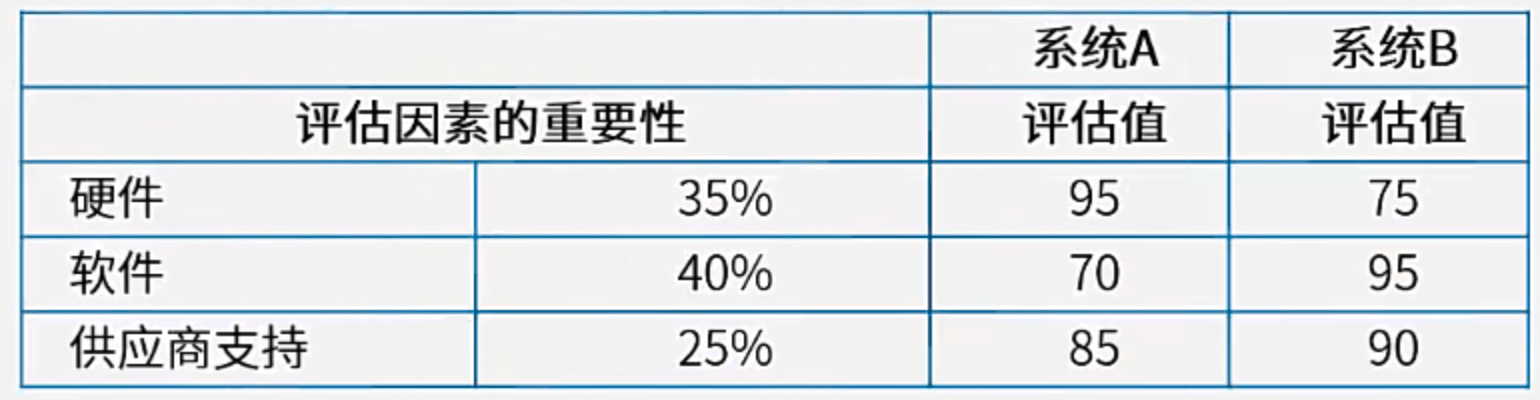
【解】由所给的决策表计算加权平均即可。
A系统：95\times 35\% + 70\times40\%+85\times25\%=82.5
B系统：75\times35\%+95\times40\%+90\times25\%=86.75
评估值越高越好，故应选B。

【例3】某企业拟进行电子商务系统的建设，有四种方式可以选择：①企业自行从头开发；②复用已有的构件来构造；③购买现成的软件产品；④承包给专业公司开发。针对这几种方式，项目经理提供了如图所示的决策树，根据此图，管理者选择建设方式的最佳决策是（?）。
A. 企业自行从头开发；B. 复用已有的构件来构造；C. 购买现成的软件产品；D. 承包给专业公司开发

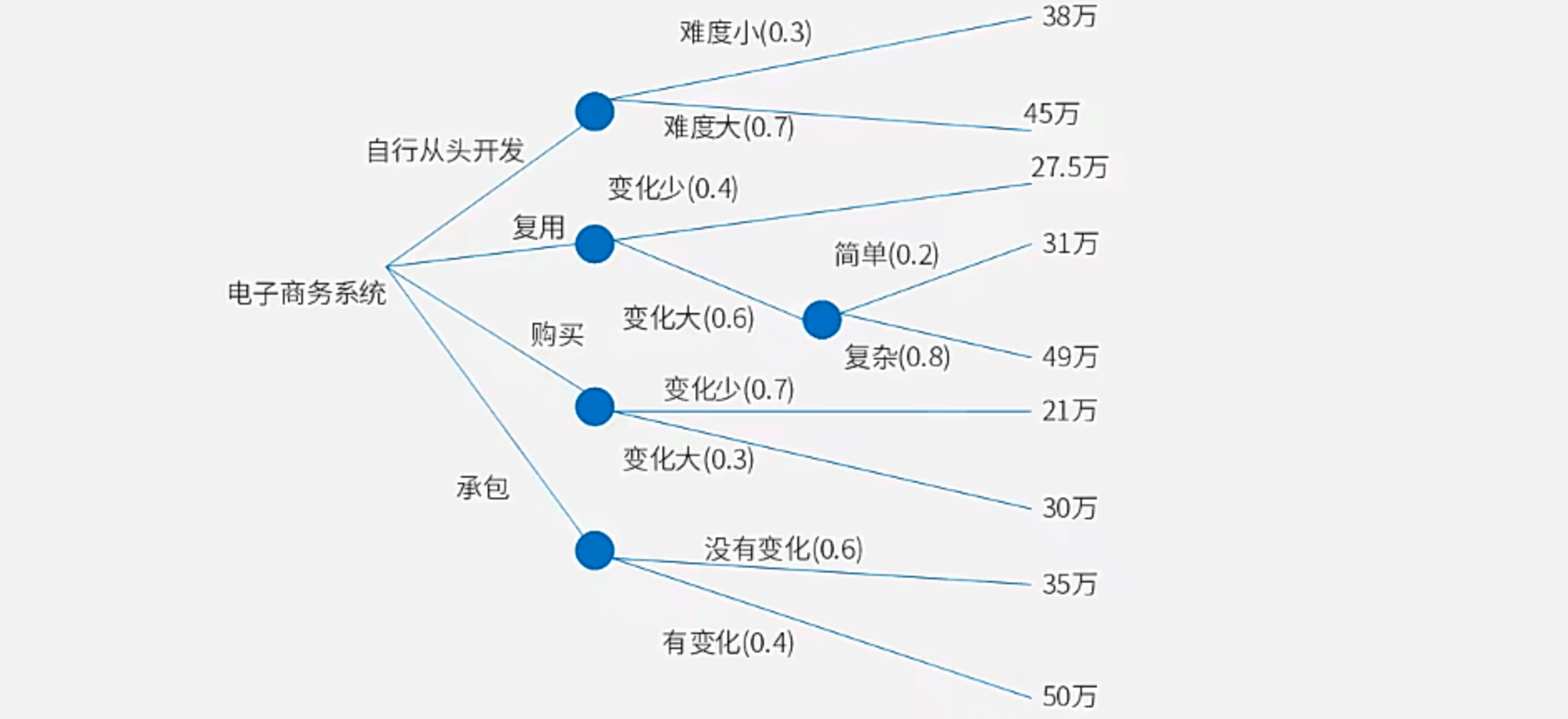
【解】由所给的决策树计算加权平均即可，注意复杂分支计算。
自行从头开发：0.3\times38+0.7\times45=11.4+31.5=42.9
复用：0.4\times27.5+(0.6\times0.2\times31+0.6\times0.8\times49)=11+(3.72+23.52)=38.24
购买：0.7\times 21+0.3\times30=14.7+9=23.7
承包：0.6\times35+0.4\times50=21+20=41
对比可得，应购买现成的软件产品。答案为C。

【例4】生产某种产品有两个建厂方案：① 建大厂，需要初期投资500万元。如果产品销路好，每年可以获利200万元；如果销路不好，每年会亏损20万元。② 建小厂，需要初期投资200万元。如果产品销路好，每年可以获利100万元；如果销路不好，每年只能获利20万元。
市场调研表明，未来2年这种产品销路好的概率为70%。如果这2年销路好，则后续5年销路好的概率上升为80%；如果这2年销路不好，则后续5年销路好的概率仅为10%。为取得7年最大总收益，决策者应（?）。
A. 建大厂，总收益超500万元；B. 建大厂，总收益略多于300万元；C. 建小厂，总收益超500万元；D. 建小厂，总收益略多于300万元
【解】建立如下决策树以及各情况的收益，分别求加权平均即可

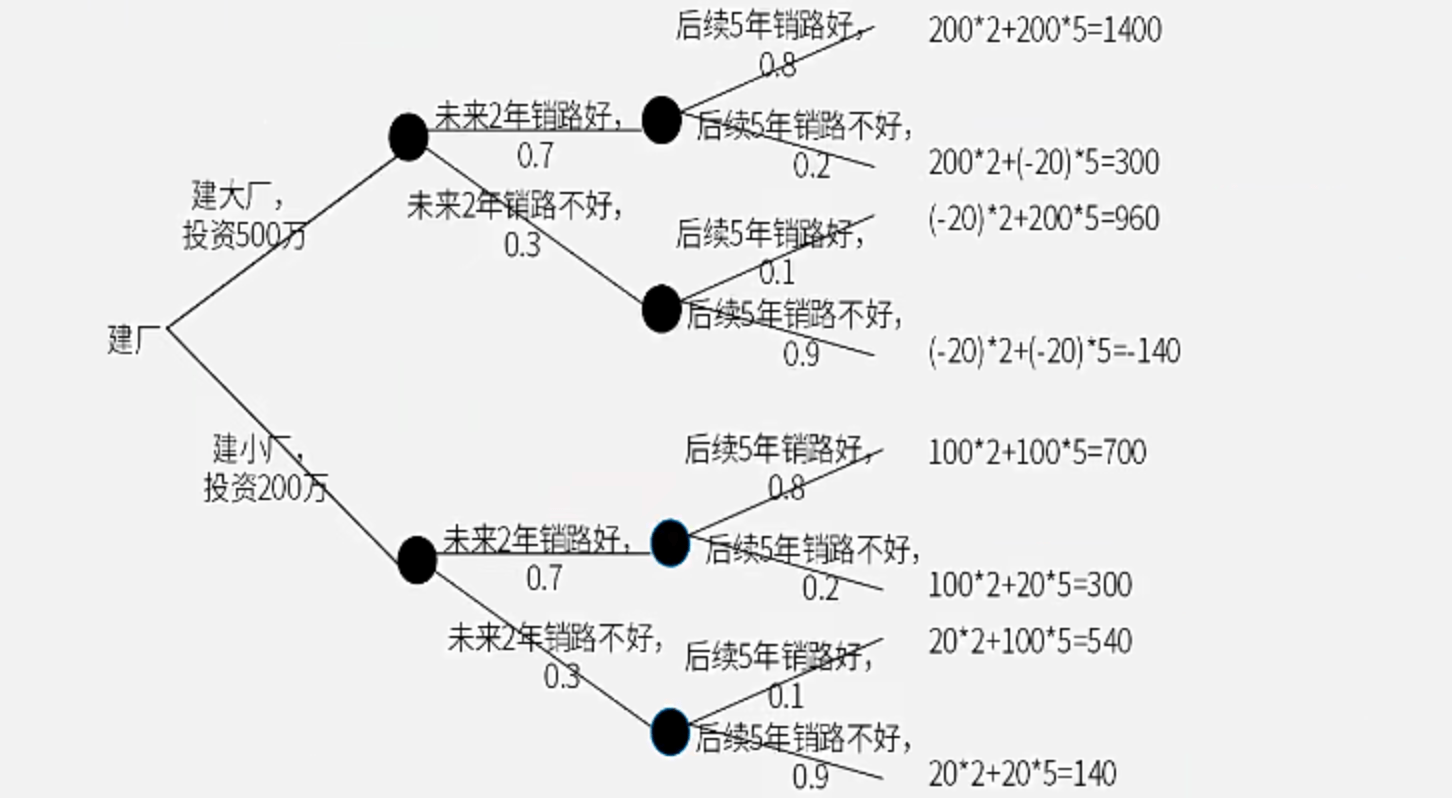
大厂：1400\times0.7\times0.8+300\times0.7\times0.2+960\times0.3\times0.1+(-140)\times0.3\times0.9-500=784+42+28.8-37.8-500=317
小厂：700\times0.56+300\times0.14+5540\times0.03+140\times0.27-200=392+42+16.2+37.8-200=288
大厂总收益高于小厂，故应建大厂，总收益未超过500万。答案为B。