常用算法代码模板（Java）——数据结构：链表、栈、队列、单调队列、模式匹配、Trie树、并查集、堆、哈希

Java算法模板系列

• Java算法模板（1）：基础算法
• Java算法模板（2）：数据结构

1 链表

用链式前向星（静态链表）实现链表的定义、遍历与增删改查。

1.1 单链表

无头单链表。元素结点地址idx从0开始分配，表尾空指针记为-1。

public class SingleLinkedList {
    static final int N = 100010;

    static int head;    // 无头单链表的头指针
    static int[] e = new int[N];    // e[i]存储结点i的值
    static int[] ne = new int[N];   // ne[i]指向结点i的后继
    static int idx;     // idx为分配给结点的"地址"

    // 初始化
    public static void init() {
        head = -1;      // 头指针初始为-1
        idx = 0;        // 这里设定第1个插入的结点在0号下标
    }

    // 头插一个数x
    public static void insertHead(int x) {
        e[idx] = x;
        ne[idx] = head;     // 后继为开始结点
        head = idx++;
    }

    // 在结点k之后插入一个数x
    public static void insert(int k, int x) {
        e[idx] = x;
        ne[idx] = ne[k];    // 后继为k的后继
        ne[k] = idx++;
    }

    // 删除头结点（需保证链表非空）
    public static void removeHead() {
        head = ne[head];
    }

    // 删除结点k之后的结点
    public static void remove(int k) {
        ne[k] = ne[ne[k]];
    }

    public static void main(String[] args) {
        // ...

        // 遍历整条链表
        for (int i = head; i != -1; i = ne[i]) {
            int u = e[i];
            // ...
        }
    }
}

1.2 双链表

带头循环双链表。规定0是头结点/左端点，只有后继；1是尾结点/右端点，只有前驱。元素结点地址idx从2开始分配，每个元素结点都不含空指针。

对于删除操作，为避免繁杂通常不直接将结点移出链表，而是通过开bool数组st[]标记结点来实现，st[i]记录结点i是否被删除。

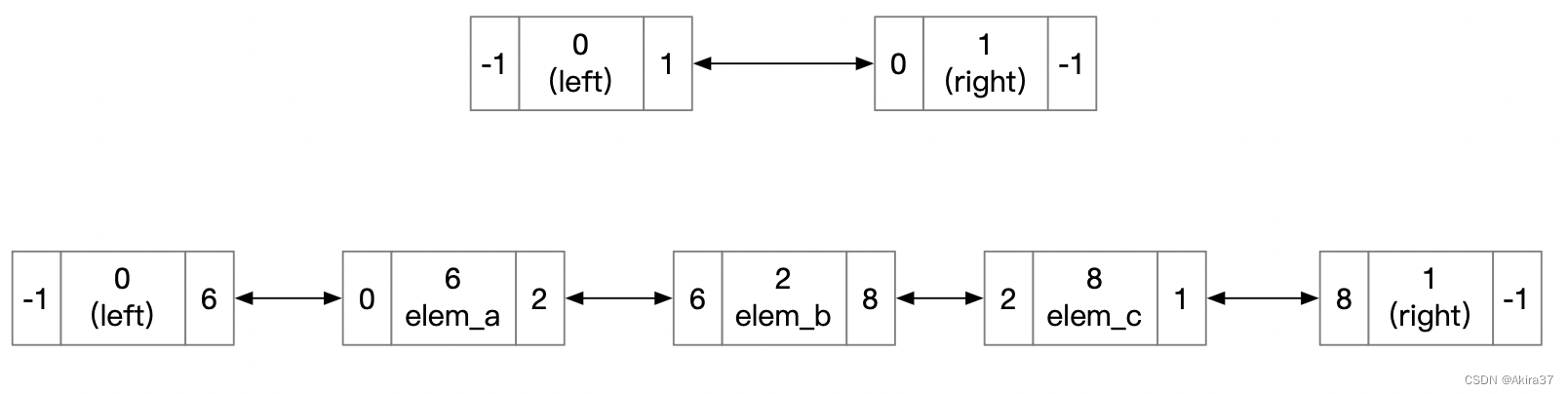
也可用来实现二叉树的二叉链表，此时无需再设循环的头结点。

public class DoubleLinkedList {
    static final int N = 100010;

    static int[] e = new int[N];
    static int[] l = new int[N];    // l[i]、r[i]分别指向结点i的前驱、后继
    static int[] r = new int[N];    // 特殊规定：0为头结点/左端点，只有后继；1为尾结点/右端点，只有前驱
    static int idx;

    // 初始化
    public static void init() {
        r[0] = 1;   // 左右端点分别指向对方
        l[1] = 0;
        idx = 2;    // 第1个结点从下标2开始存储
    }

    // 在结点k的右边插入一个数x
    public static void insertR(int k, int x) {
        e[idx] = x;
        l[idx] = k;     // 前驱为k
        r[idx] = r[k];  // 后继为k的后继
        l[r[k]] = idx;  // k后继的前驱、k的后继（须最后修改）即为该结点
        r[k] = idx++;
    }

    // 在结点k的左边插入一个数x
    public static void insertL(int k, int x) {
        insertR(l[k], x);   // 等价于在结点k的前驱（l[k]）的右边插入
    }

    // 删除结点k
    public static void remove(int k) {
        l[r[k]] = l[k];
        r[l[k]] = r[k];
    }

    public static void main(String[] args) {
        // ...

        // 遍历整条链表
        for (int i = r[0]; i != 1; i = r[i]) {
            int u = e[i];
            // ...
        }
    }
}

---

2 栈

FILO。手工数组建栈可以实现对栈内元素的随机存取。

public class Stack {
    static final int N = 100010;

    static int[] stk = new int[N];  // [0 ... N-1]
    static int tt = -1;     // 栈顶指针，初始指向-1

    // 栈顶入栈一个数
    public static void push(int x) {
        stk[++tt] = x;
    }

    // 栈顶出栈一个数
    public static void pop() {
        tt--;
    }

    // 获取栈顶的值
    public static int getTop() {
        return stk[tt];
    }

    // 判断栈是否为空
    public static boolean isEmpty() {
        return tt != -1;
    }
}

---

3 队列

FIFO

3.1 非循环队列

手工建立的非循环队列队中元素不会被覆盖，由此可以实现对队内历史元素的遍历与随机存取，或根据指针判断某些性质（如拓扑序列）。

class LinearQueue {
    static final int N = 100010;

    static int[] q = new int[N];    // [0 ... N-1]
    static int hh = 0;      // 队头初始为0
    static int tt = -1;     // 队尾初始和栈顶一样为-1

    // 队尾入队一个数
    public static void enqueue(int x) {
        q[++tt] = x;
    }

    // 队头出队一个数
    public static void dequeue() {
        hh++;
    }

    // 获取队头的值
    public static int getFront() {
        return q[hh];
    }

    // 获取队尾的值
    public static int getRear() {
        return q[tt];
    }

    // 判断队列是否为空
    public static boolean isEmpty() {
        return hh <= tt;
    }
}

3.2 循环队列

public class CircularQueue {
    static final int N = 100010;

    static int[] q = new int[N];    // [0 ... N-1]
    static int hh = 0;      // 队头和队尾指针初始均为0
    static int tt = 0;

    // 队尾入队一个数
    public static void enqueue(int x) {
        q[tt++] = x;
        if (tt == N) tt = 0;
    }

    // 队头出队一个数
    public static void dequeue() {
        hh++;
        if (hh == N) hh = 0;
    }

    // 获取队头的值
    public static int getFront() {
        return q[hh];
    }

    // 获取队尾的值
    public static int getRear() {
        return q[tt];
    }

    // 判断队列是否为空
    public static boolean isEmpty() {
        return hh != tt;
    }
}

---

4 单调队列

核心思想：及时弹出必不会作为答案的数，使得容器内各所指元素始终单调

4.1 单调栈

常见模型：找出数列中每个数左边离它最近的比它大/小的数

【例】输出数组a[1 ... n]中每个数左边离它最近的比它小的数，不存在则输出-1

public class MonotonicStack {
    static final int N = 100010;

    static int[] stk = new int[N];  // 栈中存储数组元素下标
    static int tt = -1;

    // 输出数组a[1 ... n]中每个数左边离它最近的比它小的数，不存在则输出-1
    public static void printNums(int[] a, int n) {
        // 思想：若a[x] >= a[y] (x < y)，则a[x]必不会是任何一数的答案，可直接剔除
        for (int i = 0; i < n; i++) {    // 双指针算法，i是子区间右端点
            while (tt != -1 && a[stk[tt]] >= a[i]) {
                tt--;    // 弹出既大又"远"的数
            }

            if (tt != -1) {
                System.out.print(a[stk[tt]] + " "); // 输出栈顶元素
            } else {
                System.out.print("-1 ");    // 输出-1
            }

            stk[++tt] = i;    // 入栈当前元素下标
        }
    }
}

4.2 单调队列

常见模型：找出滑动窗口中的最大值/最小值

【例】设数组a[1 ... n]中的滑动窗口长度为k，输出滑动窗口每次前移时窗口内的最小值

public class MonotonicQueue {
    static final int N = 100010;

    static int[] q = new int[N];    // 队列（双端队列）中存储数组元素下标
    static int hh = 0;
    static int tt = -1;

    // 设数组a[1 ... n]中的滑动窗口长度为k，输出滑动窗口每次前移时窗口内的最小值
    public static void printMinsOfSlidingWindow(int[] a, int n, int k) {
        // 思想：同单调栈，且应输出的最值在队头（单调）
        for (int i = 0; i < n; i++) {    // 双指针算法，i是子区间右端点
            while (hh <= tt && i - k + 1 > q[hh]) {
                hh++;    // 判断队头是否滑出窗口
            }
            while (hh <= tt && a[q[tt]] >= a[i]) {
                tt--;    // 同单调栈，队尾弹出既大又"远"的数
            }

            q[++tt] = i;    // 先将 i 从队尾入队

            if (i + 1 >= k) {
                System.out.print(a[q[hh]] + " ");    // 当窗口长度达到要求时才输出
            }
        }
    }
}

---

5 模式匹配

5.1 暴力匹配

时间复杂度：$O(n\cdot m)$

public class BruteForce {
    static String s;    // 主串
    static String p;    // 模式串

    public static void bruteForce() {
        if (s.contains(p)) {
            // ... 进行匹配成功后的操作
        }
    }
}

5.2 KMP

next数组：$\text{next}[i]=$ 以 $i$ 为终点的最大公共前后缀（此处规定包含 $i$ ）的长度

时间复杂度：$O(n+m)$

public class KMP {
    static final int N = 100010;

    static char[] s = new char[N];  // 主串 s[1 ... n]
    static char[] p = new char[N];  // 模式串 p[1 ... m]（必须从下标 1 开始存储字符）
    static int n;   // 主串长度为n
    static int m;   // 模式串长度为m
    static int[] ne = new int[N];   // next 数组

    // 初始化主串和模式串
    public static void initStr() {
        Scanner sc = new Scanner(System.in);
        sc.next();  // 读取不带空格的字符串作为主串
        s = (" " + sc.next()).toCharArray();    // 从下标1开始读取主串
        p = (" " + sc.next()).toCharArray();    // 从下标1开始读取模式串
        n = s.length - 1;   // 获取主串有效存储长度 (s[0]用于填充)
        m = p.length - 1;   // 获取模式串有效存储长度 (p[0]用于填充)
    }

    // 求模式串p的next数组：p对p自己作KMP匹配
    public static void initNext() {
        for (int i = 2, j = 0; i <= m; i++) {    // ne[1]=0，故i从2开始遍历
            while (j > 0 && p[i] != p[j + 1]) {
                j = ne[j];    // j回溯
            }
            if (p[i] == p[j + 1]) {
                j++;        // 匹配成功则表明得到了以当前i为终点的最大公共前后缀的长度
            }
            ne[i] = j;        // 记录next数组
        }
    }

    // KMP匹配
    public static void kmp() {
        for (int i = 1, j = 0; i <= n; i++) {    // 始终与j的下一位 (j + 1) 作匹配
            while (j > 0 && s[i] != p[j + 1]) {
                j = ne[j];    // j回溯
            }
            if (s[i] == p[j + 1]) {
                j++;        // 匹配成功时 j 走至下一位
            }

            if (j == m) {    // 匹配成功的操作
                // ... 进行匹配成功后的操作
                j = ne[j];    // 若要求找到所有匹配点，则 j 继续回溯、匹配
            }
        }
    }
}

---

6 Trie树

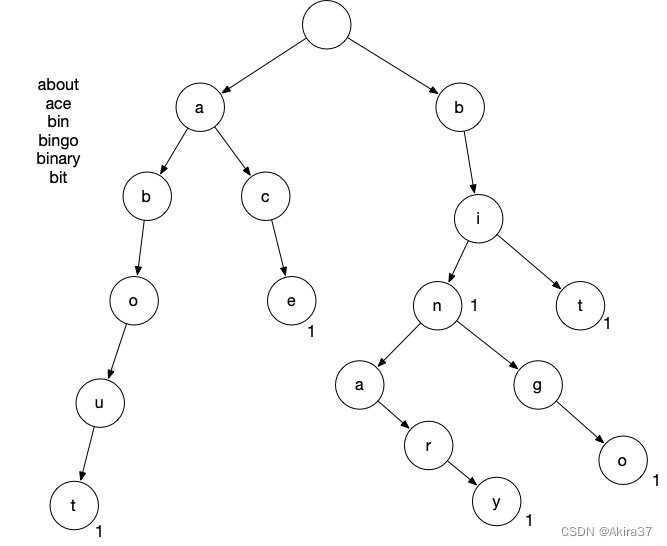
字典树（Retrieval Tree, Trie Tree）用于高效存储和查找字符串集合。

AC自动机为追加了fail指针的Trie树，算法思想参考KMP。

public class TrieTree {
    static final int N = 100010;

    static int[][] son = new int[N][26];    // son[p][u]记录结点p的第u个子结点
    static int[] cnt = new int[N];  // cnt[p]存储以结点p结尾的单词数量
    static int idx = 0; // idx初始为0（0号点既是根结点，又是空结点）

    // 插入一个字符串
    public static void insert(String str) {
        int p = 0;    // 从根结点0起遍历Trie的指针
        for (int i = 0; i < str.length(); i++) {
            int u = str.charAt(i) - 'a';    // 将字符转换为对应的索引
            if (son[p][u] == 0) {
                son[p][u] = ++idx;    // 不存在则创建该子结点
            }
            p = son[p][u];    // 更新指针走向当前子结点
        }
        cnt[p]++;    // p最终指向字符串末尾字母，p计数器自增
    }

    // 查询字符串出现的次数
    public static int query(String str) {
        int p = 0;    // 从根结点开始
        for (int i = 0; i < str.length(); i++) {
            int u = str.charAt(i) - 'a'; // 将字符转换为对应的索引
            if (son[p][u] == 0) {
                return 0;    // 不存在则直接返回0
            }
            p = son[p][u];    // 更新指针至下一个结点
        }
        return cnt[p];    // p最终指向字符串末尾字母，返回数量
    }
}

---

7 并查集

使用树的双亲表示法顺序存储，p[x]存储结点x的父结点（经过路径更新后变为该结点所属集合的根结点/祖宗结点）。若p[x] == x（或find(x) == x），则x为该集合的根结点。

判断结点a和b是否在同一集合：find(a) == find(b)

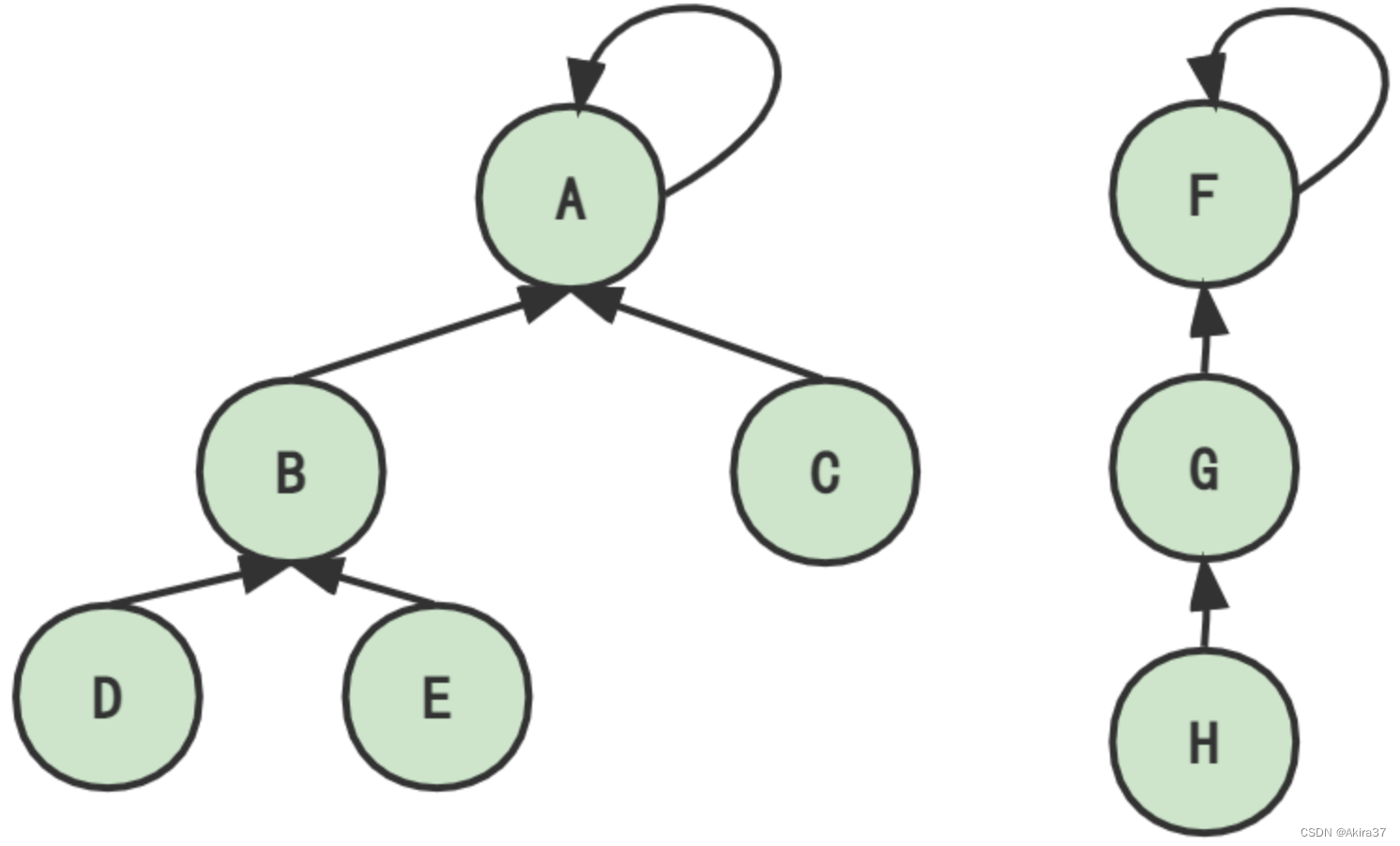
7.1 朴素并查集

public class SimpleDisjointSet {
    static final int N = 100010;

    static int n;
    static int[] p = new int[N];    // p[1 ... n]，p[i]存储结点i的祖先（路径压缩后则为根结点）

    // 初始化
    public static void init() {
        for (int i = 1; i <= n; i++) {
            p[i] = i;
        }
    }

    // 并查集核心操作：返回结点x所属集合的根结点，并进行路径压缩
    public static int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    // 合并结点a和b所在集合：将a并至b
    public static void union(int a, int b) {
        p[find(a)] = find(b);   // 将a的根接在b的根之后
    }
}

7.2 维护集合大小的并查集

结点a所属集合的大小：cnt[find(a)]

public class DisjointSetWithSize {
    static final int N = 100010;

    static int n;
    static int[] p = new int[N];
    static int[] cnt = new int[N];  // cnt[i]存储根结点i的集合中结点数（仅根结点的cnt有意义）

    // 初始化
    public static void init() {
        for (int i = 1; i <= n; i++) {
            p[i] = i;
            cnt[i] = 1; // 初始化各结点为根，其所属集合大小为1
        }
    }

    // 并查集核心操作
    public static int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    // 合并结点a和b所在集合：将a并至b
    public static void union(int a, int b) {
        if (find(a) == find(b)) return; // 若已在同一集合内则跳过

        cnt[find(b)] += cnt[find(a)];   // 需将a所属集合的大小加至b
        p[find(a)] = find(b);
    }
}

7.3 维护到祖宗结点距离的并查集

public class DisjointSetWithDistance {
    static final int N = 100010;

    static int n;
    static int[] p = new int[N];
    static int[] d = new int[N];    // d[i]存储结点i到其根结点p[i]的距离

    // 初始化
    public static void init() {
        for (int i = 1; i <= n; i++) {
            p[i] = i;
            d[i] = 0;   // 初始化全为0
        }
    }

    // 并查集核心操作
    public static int find(int x) {
        if (p[x] != x) {
            int u = find(p[x]);    // u临时记录根结点
            d[x] += d[p[x]];    // 更新x到根p[x]的路径长度
            p[x] = u;
        }
        return p[x];
    }

    // 合并结点a和b所在集合：将a并至b
    public static void union(int a, int b) {
        p[find(a)] = find(b);
    }

    // 根据具体问题，初始化根find(a)的偏移量
    public static void setDistance(int a, int distance) {
        d[find(a)] = distance;
    }
}

---

8 堆

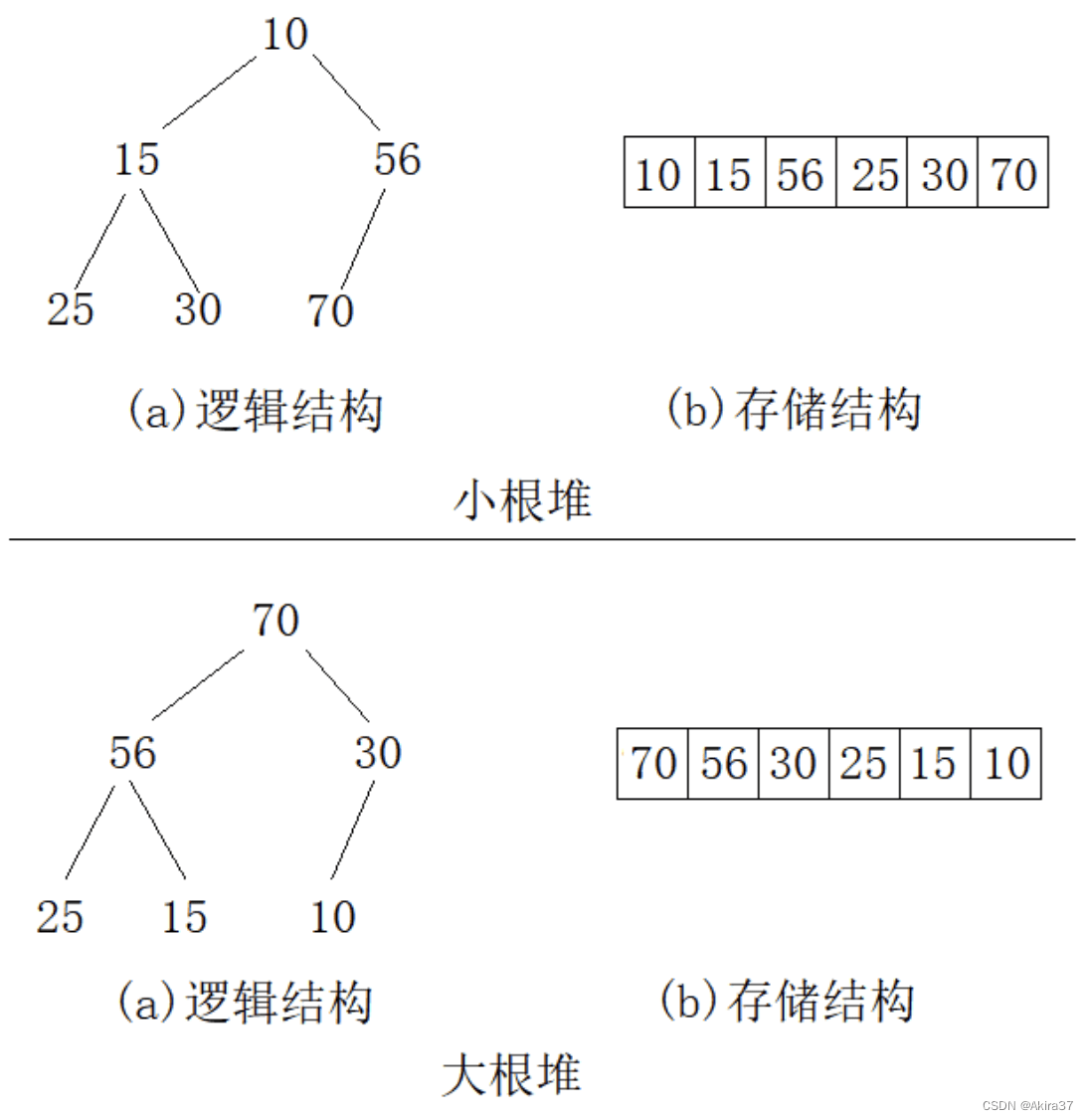
8.1 优先队列

java中PriorityQueue默认为小根堆，因此创建大根堆需要使用Collections.reverseOrder()作为构造参数

PriorityQueue<Integer> max_heap = new PriorityQueue<>(Collections.reverseOrder()); // 大根堆（）
PriorityQueue<Integer> min_heap = new PriorityQueue<>(); // 小根堆

8.2 数组堆

可实现堆中任意元素的插入删除操作，并建立与插入序列之间的映射关系。

class Heap {
    static final int N = 100010;

    static int[] h = new int[N];    // 小根堆h[1 ... cnt]，h[1]为堆顶/最小值，结点u的左右儿子（若存在）分别为2u、2u+1
    static int cnt;
    static int[] ph = new int[N];    // ph[k]映射插入序列中第k个点到堆中的下标u (Position-Heap)
    static int[] hp = new int[N];    // hp[u]映射堆中结点u到插入序列中的序号k (Heap-Position)
    static int idx = 0;

    // 堆swap函数：交换堆中两个结点a和b的所有信息（若不建立映射则只需编写swap函数即可，略）
    public static void heapSwap(int a, int b) {
        // cpp:
        // swap(ph[hp[a]], ph[hp[b]]);
        // swap(hp[a], hp[b]);
        // swap(h[a], h[b]);
    }

    // 向下调整：一路向下交换结点u与其较小的儿子
    public static void down(int u) {
        int t = u;        // 记录u、2u、2u+1三个结点中的最小值结点编号
        if (2 * u <= cnt && h[2 * u] < h[t]) {
            t = 2 * u;
        }
        if (2 * u + 1 <= cnt && h[2 * u + 1] < h[t]) {
            t = 2 * u + 1;
        }

        if (t != u) {
            heapSwap(u, t);
            down(t);
        }
    }

    // 向上调整：一路向上交换结点u与其父结点
    public static void up(int u) {
        while (u / 2 != 0 && h[u / 2] > h[u]) {
            heapSwap(u / 2, u);
            u >>= 1;
        }
    }

    // 插入一个数x
    public static void insert(int x) {
        cnt++;
        idx++;
        ph[idx] = cnt;
        hp[cnt] = idx;
        h[cnt] = x;
        up(cnt);
    }

    // 删除最小值/堆顶元素
    public static void removeTop() {
        heapSwap(1, cnt);
        cnt--;
        down(1);
    }

    // 删除第k个插入的元素
    public static void remove(int k) {
        int u = ph[k];
        heapSwap(u, cnt);
        cnt--;
        up(u);  // up、down只会执行其中一个
        down(u);
    }

    // 修改第k个插入的元素为x
    public static void change(int k, int x) {
        int u = ph[k];
        h[u] = x;
        up(u);  // up、down只会执行其中一个
        down(u);
    }
}

---

9 哈希

HashSet、HashMap

9.1 一般哈希

N最好取质数，使得冲突概率尽可能低

若要删除，则可额外开bool数组标记各地址元素状态来表示是否被删

9.1.1 拉链法

public class ChainingHashTable {
    static final int N = 100010;

    static int[] h = new int[N];
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int idx = 0;

    // 初始化
    public static void init() {
        Arrays.fill(h, -1);
    }

    // 向哈希表中插入一个数
    public static void insert(int x) {
        int t = (x % N + N) % N;    // C++、Java的负数取余运算：(-n) mod k = -(n mod k)
        e[idx] = x;
        ne[idx] = h[t];
        h[t] = idx++;
    }

    // 在哈希表中查询某个数是否存在
    public static boolean find(int x) {
        int t = (x % N + N) % N;
        for (int i = h[t]; i != -1; i = ne[i]) {    // 遍历整条链表 h[t]
            if (e[i] == x) return true;
        }
        return false;
    }
}

9.1.2 开放寻址法

数组长度应开到最大数据量的2~3倍

public class OpenAddressingHashTable {
    static final int N = 100010;
    static final int INF = 0x3f3f3f3f;  // 若为INF则表示该哈希值的元素不在哈希表内

    static int[] h = new int[N];

    // 初始化
    public static void init() {
        Arrays.fill(h, INF);    // 初始化为无穷
    }

    // 若x在哈希表中，返回x的下标；否则返回x应该插入的位置
    public static int find(int x) {
        int t = (x % N + N) % N;
        while (h[t] != INF && h[t] != x) { // 若已存在该哈希值的元素且该元素不等于 x
            t++;
            if (t == N) {
                t = 0; // 如果超出范围，则循环回到 0
            }
        }
        return t; // 返回找到的位置
    }
}

9.2 字符串哈希

字符串前缀哈希法：快速判断两段字符串是否相等（不考虑冲突）

• 核心思想：将字符串看成 $P$ 进制数，$P$ 的经验值是 $131$ 或 $13331$ ，取这两个值的冲突概率极低
• 取模的数可选用$2^{62}-1$

public class StringHash {
    static final int N = 100010;
    static final long P = 131;
    static final long MOD = (1L << 62) - 1;

    static char[] str = new char[N];    // 待哈希字符串 str[0 ... n - 1]
    static int n;   // 字符串的长度
    static long[] h = new long[N];      // h[k]存储字符串前k个字母的哈希值（前缀和）
    static long[] p = new long[N];      // p[k]存储 P^k mod MOD

    // 预处理前缀哈希
    public static void init() {
        p[0] = 1;
        for (int i = 1; i <= n; i++) {
            h[i] = (h[i - 1] * P + str[i - 1]) % MOD; // 注意此处str从0开始索引
            p[i] = p[i - 1] * P % MOD;
        }
    }

    // 计算子串str[l ... r]的哈希值（注意h、p的定义）
    public static long get(int l, int r) {
        l++;
        r++;
        return (h[r] - h[l - 1] * p[r - l + 1] % MOD + MOD) % MOD; // 注意防止h[l - 1] * p[r - l + 1]为负
    }
}